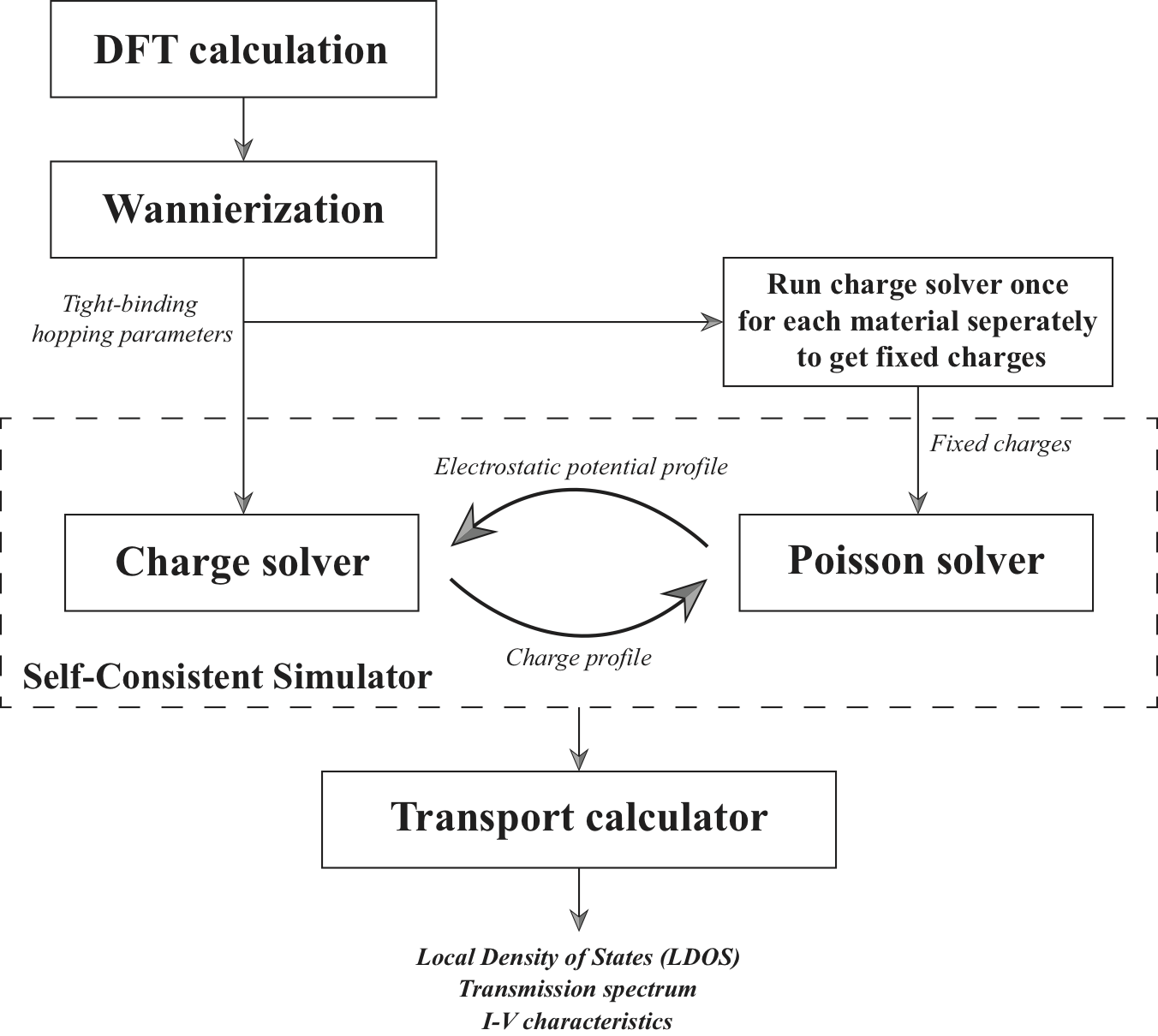
Swan (Self-consistent Wannier-function-based quantum transport solver) is an open-source C++ software suitable for large-scale atomistic simulations of electronic structures and transport properties for nano-devices. By using a Wannier function basis (as implemented in the Wannier90 package) to accurately describe the electronic bands, our code is able to efficiently model device structures with first-principles accuracy at a minimal cost of tight-binding calculations. It couples the Keldysh non-equilibrium Green's function formalism and Poisson solver to generate the inhomogeneous charge densities self-consistently with the electrostatic potential profile for the simulated device region. The parallel implementation of the code uses the standard Message Passing Interface (MPI). We depicted our simulation pipeline as below:
For more details, please refer to the related paper "Quantum electron transport in ohmic edge contacts between two-dimensional materials" (https://doi.org/10.1021/acsaelm.9b00095).
Author: Wushi Dong ([email protected]) of the Physics Department at The University of Chicago. (Advisor: Peter B. Littlewood)
The author would like to acknowledge the C++ linear algebra library Armadillo.
Download and install the Armadillo package via the webpage:
http://arma.sourceforge.net/download.html
Install Swan by running the "install.sh" file provided in the package:
sh install.sh
If you want to run the code in parallel, please make sure that relevant MPI implementation is installed.
To demonstrate the usage of our code, we provide an example run which simulates the 2D edge contact structure studied in our paper (https://arxiv.org/abs/1811.02135).
To run this example: (Make sure MPI is installed since this example will use mpirun)
cd example_run/
sh run.sh
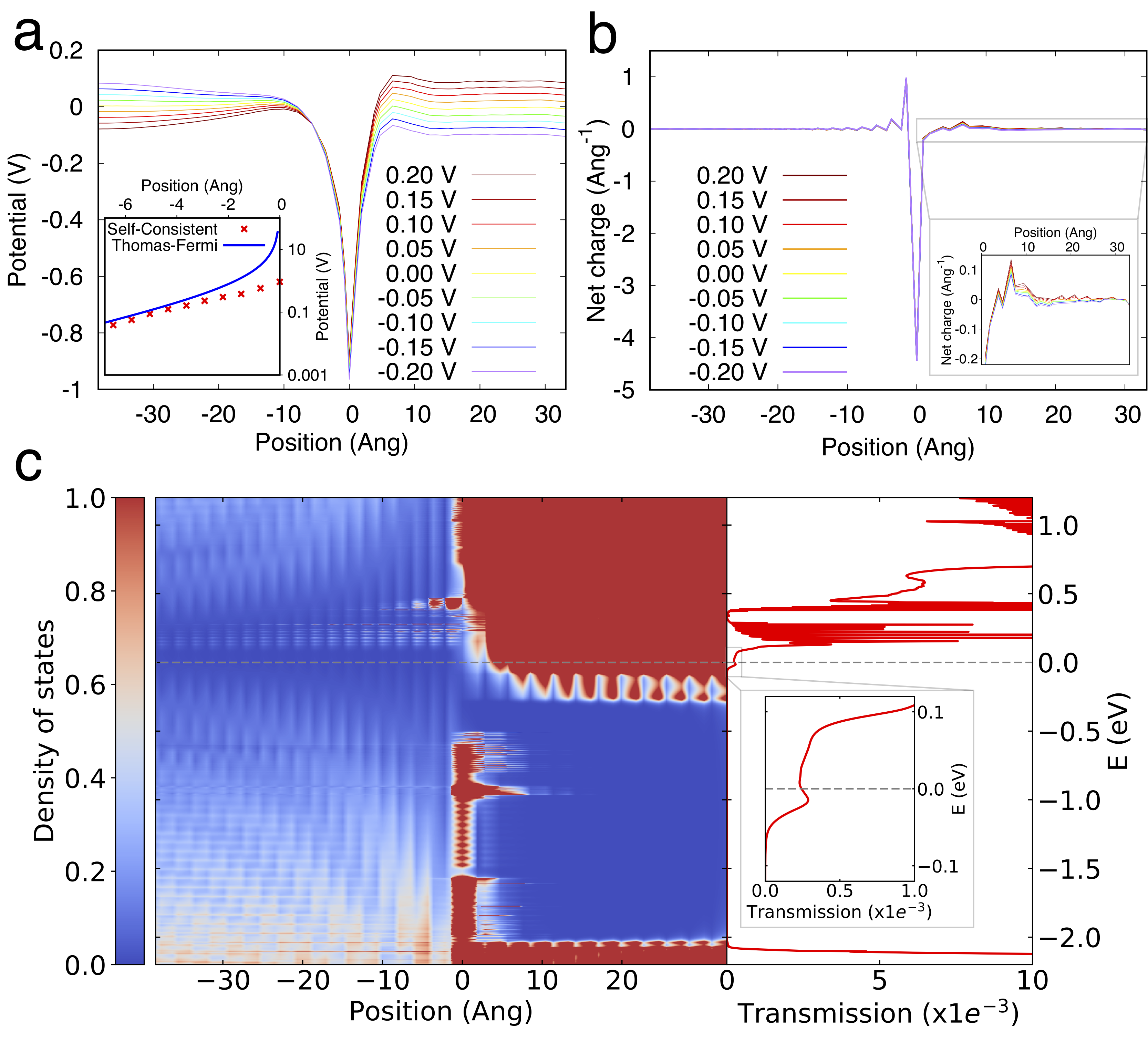
We present in the following two results that one can extract from the above simulation. The first figure shows the converged electrostatic potential profiles under different temperatures. (Inset: comparison between our self-consistent simulation results and analytical predictions using Thomas-Fermi theory.)
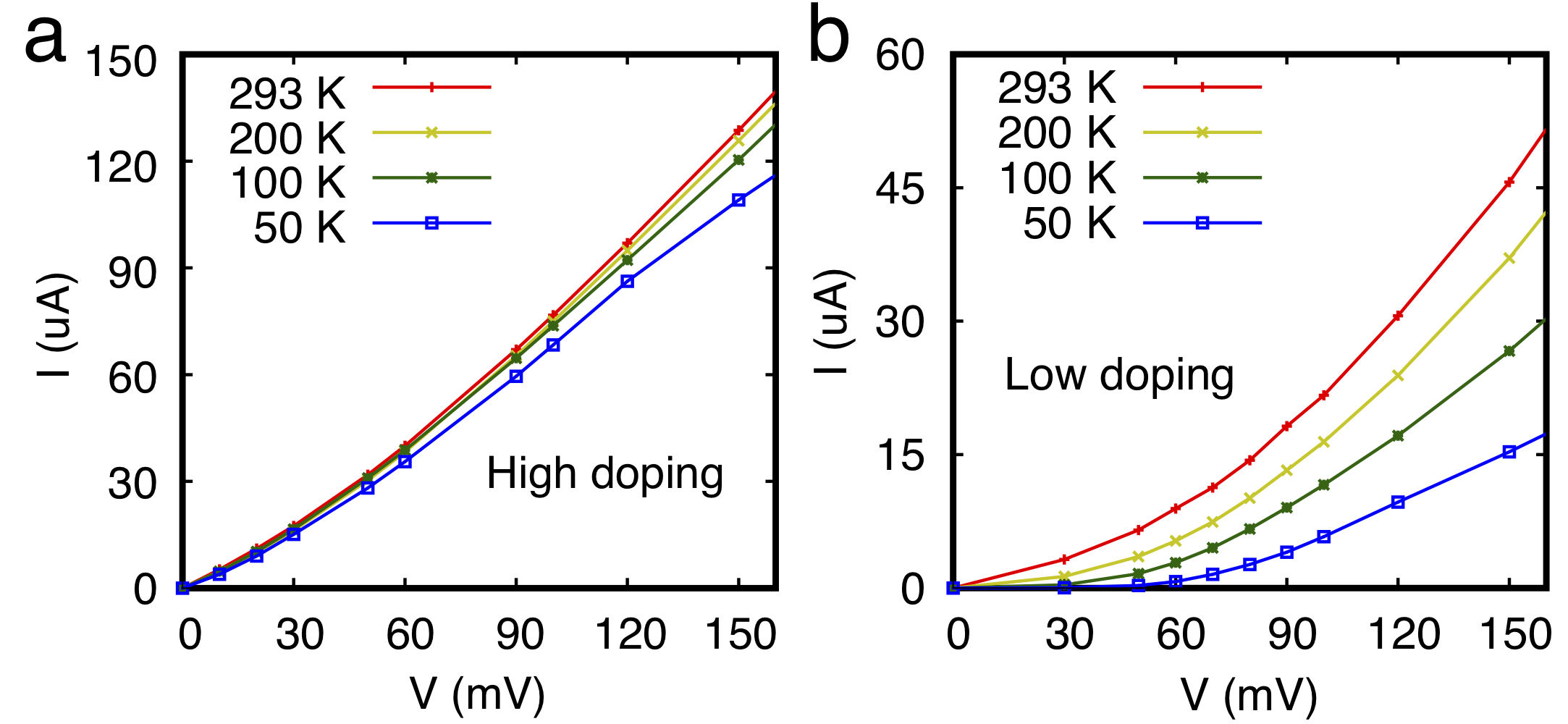
The second one is the I-V characteristics under different temperatures for high and low doping levels respectively. From this figure, one can see how doping levels affect the ohmic behavior of the edge contact.