Compute Flattened State Transition Map

This algorithm flattens the state transitions in a state machine definition. By flattening transitions, we simplify the code generation and runtime logic.

Input

1. A state machine definition smd.

2. A state machine analysis data structure sma representing the results of analysis so far.

Output

1. sma with the flattened state transition map updated.

Diagrams

The following diagrams illustrate how state transitions are flattened.

State Transitions to States Other Than Parents of Self

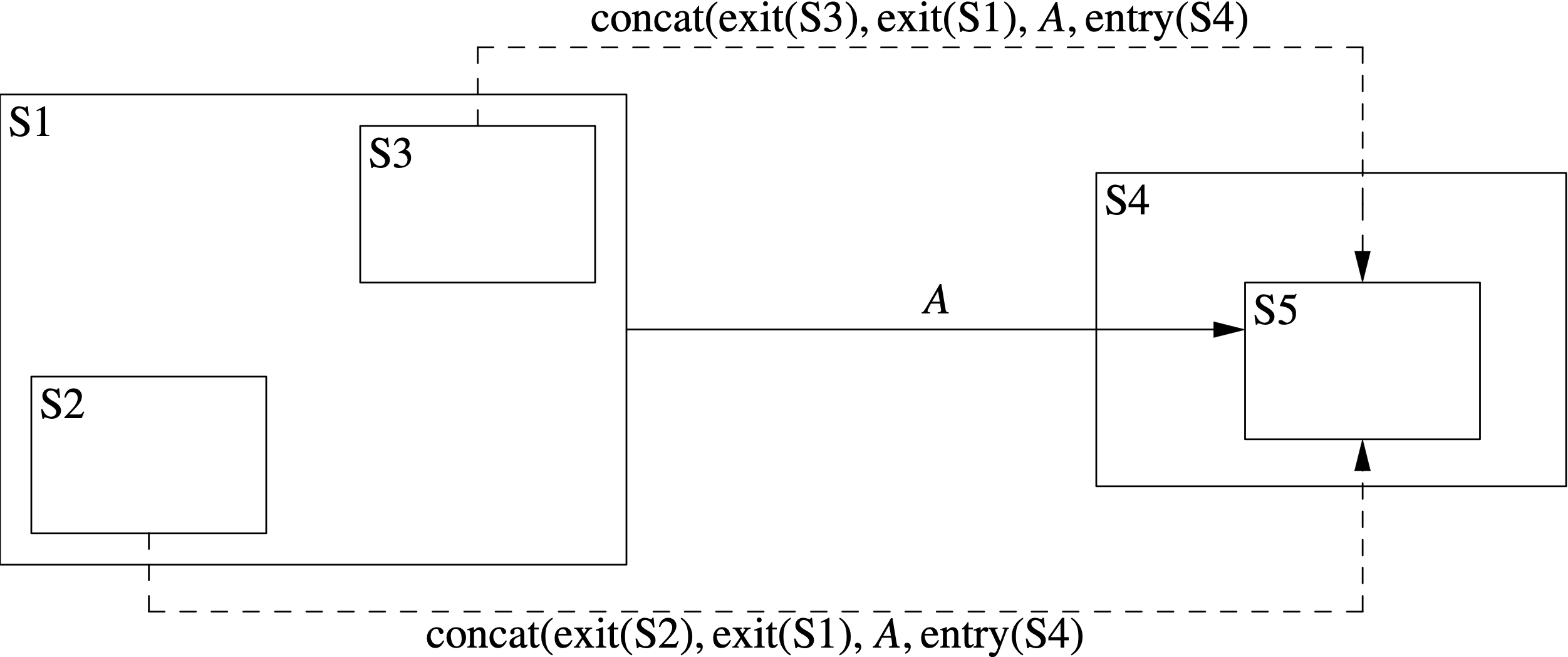
Figure 1 shows how transitions are flattened where, after the flattening, the target state T is not a transitive parent of the source state S (i.e., T is not S, or a parent of S, or a parent of a parent of S, etc.). In this example, S1 is a state with substates S2 and S3. S4 is a state with substate S5.

The solid left-to-right arrow represents a transition T in the hierarchical state machine from S1 to S5 with actions A. T generates each of the flattened transitions represented by the dashed arrows. Neither of the arrows goes from a state S to a transitive parent of S. For each dashed arrow, the action list is the concatenation of the action lists shown. In these lists, exit(S) represents the list of exit functions specified by S, and similarly for entry(S).

Figure 1. State transitions to states other than parents of self.

Note the following:

1. Each flattened transition goes from a leaf state but not necessarily to a leaf state.

2. In general, T generates the transitions out of S2 and S3 as shown. However, if the hierarchical state machine specifies a transition T' out of S2, and T' is triggered by the same signal as T, then T' overrides T; and similarly for a transition T'' out of S3. This rule is called behavioral polymorphism.

State Transitions to Parents of Self

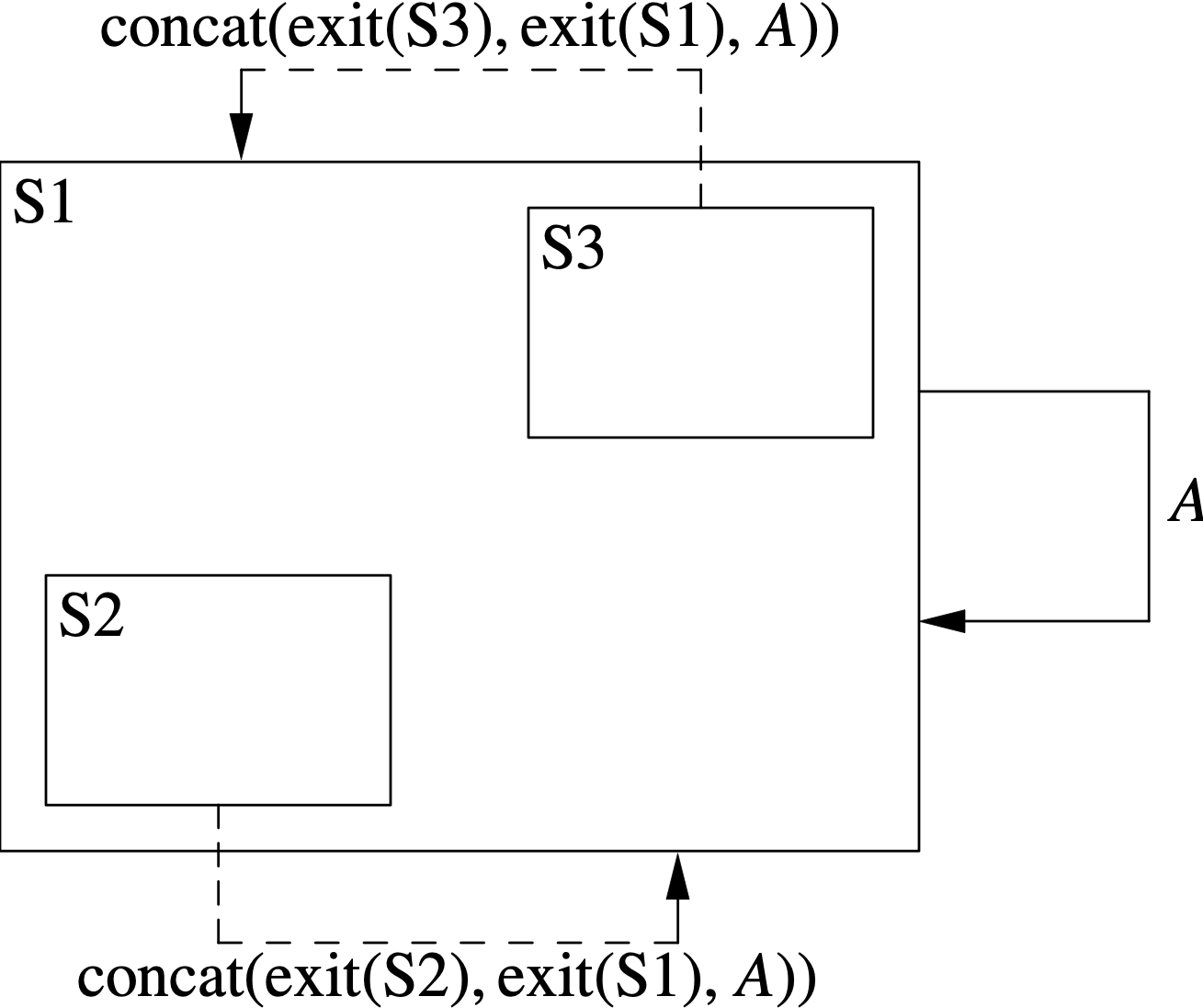
Figure 2 shows how transitions are flattened where, after the flattening, the transition goes from a state S to a transitive parent of S. Again S1 is a state with substates S2 and S3.

The solid clockwise arrow represents a transition T in the hierarchical state machine from S1 to itself with actions A. T generates each of the flattened transitions represented by the dashed arrows. Each arrow goes from a state S to a transitive parent of S. For each dashed arrow, the action list is the concatenation of the action lists shown.

Figure 2. State transitions to parents of self.

Note the following:

1. When a flattened transition goes from a state S to a transitive parent P of S, we exit and re-enter P. For purposes of this rule, S is a transitive parent of itself.

2. Again the transition out of S2 will be be overridden if there is a transition specified in S2 on the same signal, and similarly for S3.

State Transitions to Choices

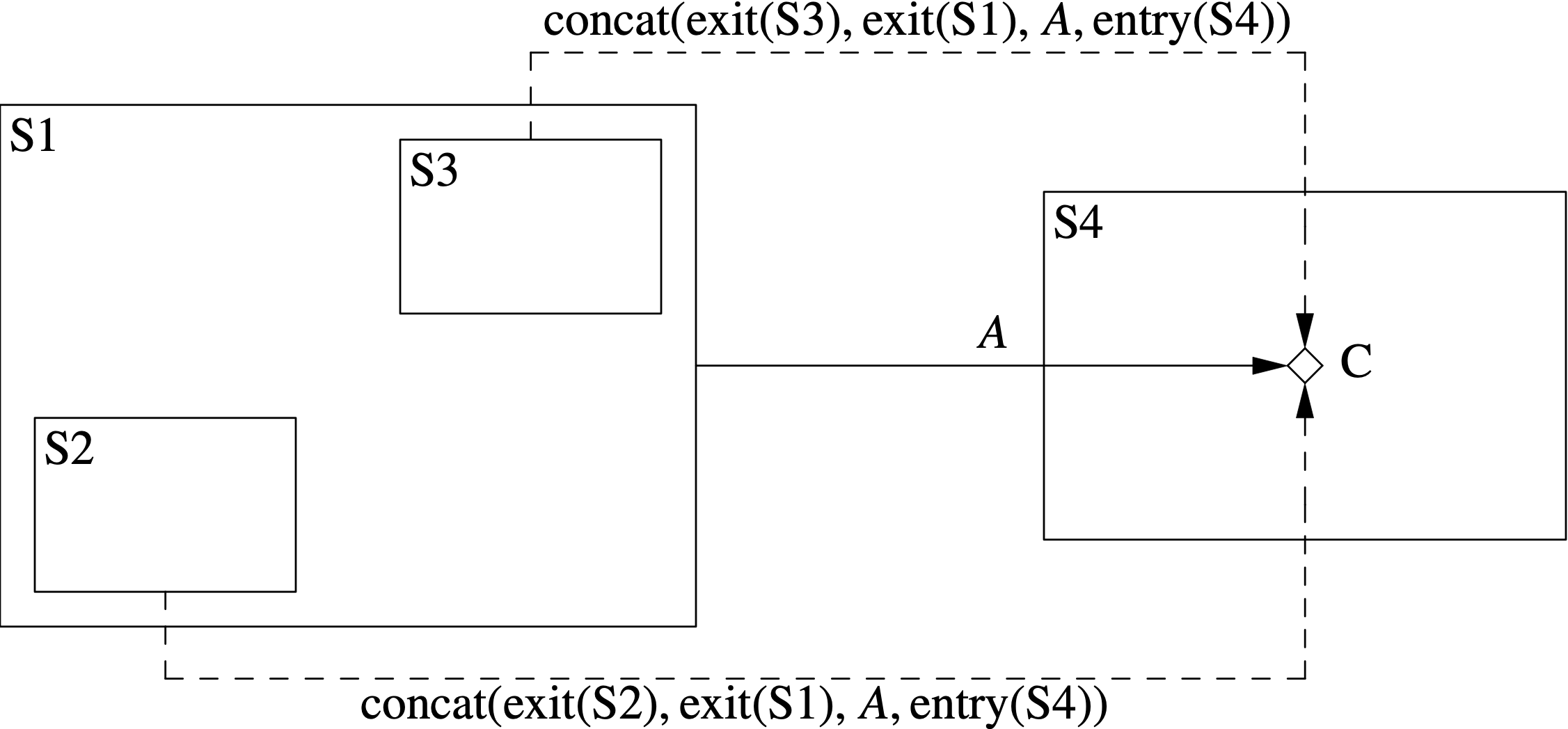
Figure 3 shows how state transitions to choices are flattened. Again S1 is a state with substates S2 and S3. S4 is a state with a choice definition C. The solid left-to-right arrow represents a transition T in the hierarchical state machine from S1 to C with actions A. T generates each of the flattened transitions represented by the dashed arrows.

Figure 3. State transitions to choices.

Note the following:

1. Each flattened transition goes from a leaf state to a choice.

2. Choices do not have entry actions or substates.

3. Again the transition out of S2 will be be overridden if there is a transition specified in S2 on the same signal, and similarly for S3.

Internal Transitions

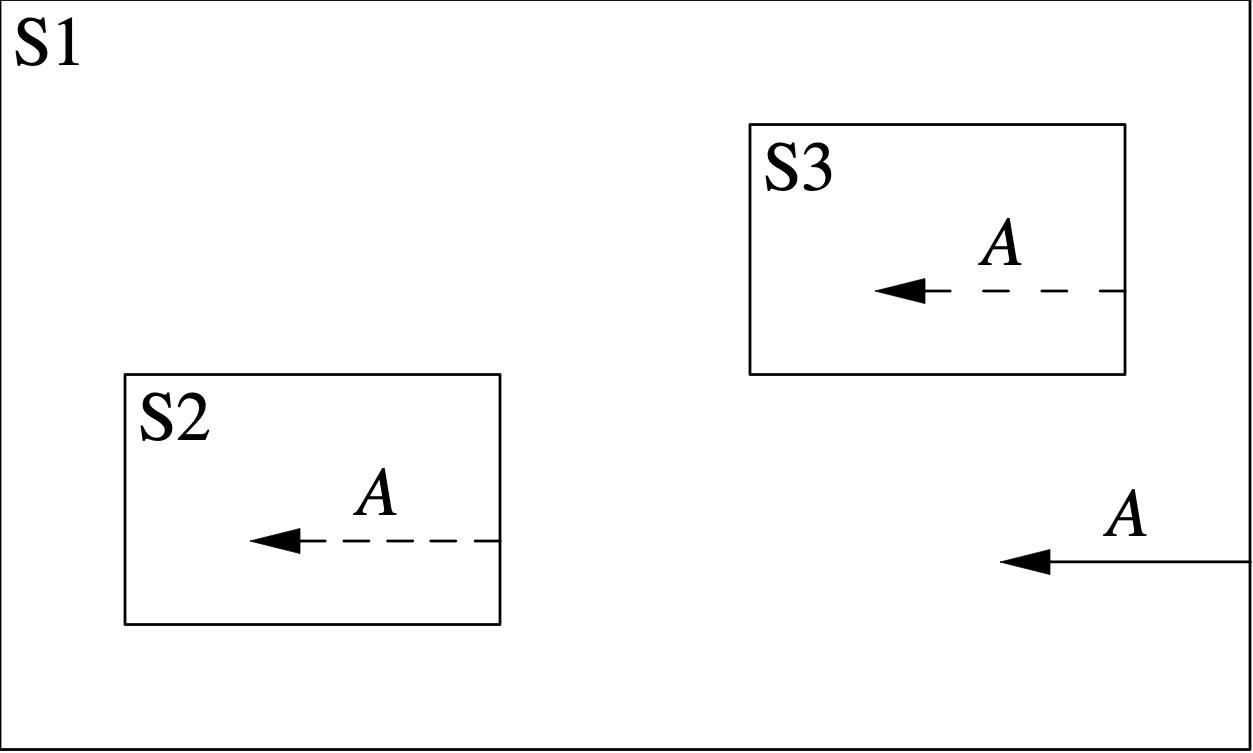
Figure 4 shows how internal state transitions are flattened. Again S1 is a state with substates S2 and S3.

The solid arrow represents an internal transition T in the hierarchical state machine from S1 to itself with actions A. T generates each of the flattened internal transitions represented by the dashed arrows.

Figure 4. Internal transitions.

Note the following:

1. When flattening an internal transition, we do exit or enter any states.

2. Again the transition from S2 will be be overridden if there is a transition specified in S2 on the same signal, and similarly for S3.

Procedure

1. Let stm be the signal-transition-map of sma.

2. Let fstm be the flattened state transition map of sma.

3. Set each of stm and fstm to the empty map.

4. Visit each state definition that is a direct member of smd.

Visiting State Definitions

1. Let sd be the state definition being visited.

2. Let stm' = stm.

3. For each state transition specifier sts in sd

   1. Let s be the signal of sts, let g be the optional guard of sts, and let A be the actions of sts.

   2. If sts specifies an internal transition (i.e., sts has actions but no target), then let t be the internal transition with actions A.

   3. Otherwise let t be the external transition whose actions are A and whose target is the target of sts.

   4. Update stm so that it maps s to (g,t). If any preexisting transition is mapped to s, it is overridden. Because we walk the AST in depth-first order, a transition specified lower in the tree overrides any transition on the same signal specified higher in the tree. Thus the algorithm respects behavioral polymorphism.

4. If sd is a leaf state, then

   1. For each signal s in stm

      1. Let (g,t) = stm(s).

      2. Construct the flattened transition t' with source sd and transition t.

      3. If fstm(s) does not exist, then set fstm(s) to the empty map.

      4. Add the mapping from sd to (g,t') to fstm(s).

5. Otherwise for each child state definition sd' of sd, visit sd'.

6. Set stm = stm'.