This document is a work in progress

MaxEnt source code review

Source code review of Tsuruoka's C++ library for maximum entropy classification (see http://www.nactem.ac.uk/tsuruoka/maxent/).

Introduction

On his website, Tsuruoka proposed a C++ library for maximum entropy classification. In order to get a better and deeper understanding of implementation details, I propose here a simple code review. The code base is relatively small (around 2500 lines of code). Those notes are primary destined for my personal use and reflect my current understanding. I propose them here, in case where that could help someone.

This article is divided in three parts:

• The core
• Optimization methods
• Postagging example

But, before digging ahead, let's get an overview of the code base.

Overview

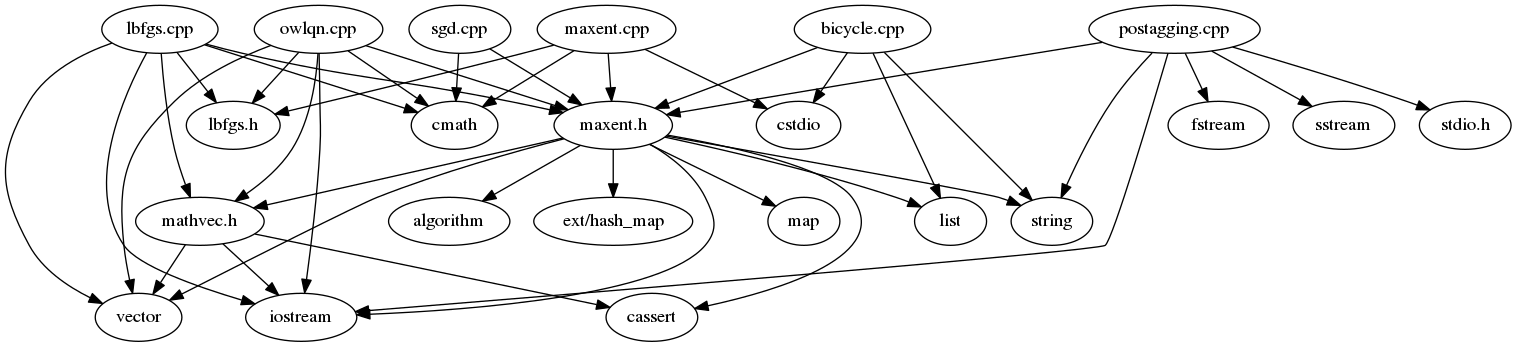
Using Rexdep, we can obtain the following directed graph of dependencies:

The core of the library are the header maxent.h, and its implementation maxent.cpp. In this core, the fundamental structures and functions of the learning task are defined (training set, functions for computing of objective, etc.). The following section will discuss some of these aspects.

Besides that, three optimization methods are proposed:

• lbfgs.cpp: the very efficient BFGS algorithm in limited memory version;
• owlqn.cpp: a variant of BFGS for L1-regularized models;
• sgd.cpp: the classic stochastic gradient descent;

Note that, due to their shared nature, lbfgs.cpp and owlqn.cpp include both the header lbfgs.h.

Two classification examples are proposed:

• bicycle.cpp: binary classification between cars and bicycles given simple features. This example is made to just figure out the basic principles;
• postaggin.cpp: the classic task which aims at identifying the right part-of-speech (POS) for a given token. A little dataset of 200 sentences is given to train and test new models;

A word about mathvec.h

The mathvec.h describes the class Vec which extends the possibilities of vector<double>: the operators (e.g. <<, binary +, etc.) are overloaded and some facilities are in place for computing the dot product and the vector projection. Those elements are used in lbfgs.cpp, owlqn.cpp and maxent.h.

In this case, the optimization aspect is taken into account. For instance, the dot production function is inlined, in order to save CPU registers and increase the efficiency of the operation.

inline double dot_product(const Vec & a, const Vec & b)
{
  double sum = 0;
  for (size_t i = 0; i < a.Size(); i++) {
    sum += a[i] * b[i];
  }
  return sum;
}

The core

The class ME_Model is the core of the library. This is reflected in the space that class takes in maxent.h (about 80% of the written source code). A couple of nested structures are defined inside ME_Model. Note that nesting does not imply other relations than a shared scope for the nested structures. Inheritance or composition are not involved, unless they are explicitly stated. The following figure gives an insight about the global architecture:

ME_Sample and Sample

The structure ME_Sample records the observations. Each ME_Sample have its own features. There are two kinds of features: binary (vector<string>) and real-valued (vector<pair<string, double>>) features.

When the ME_Sample records are added to the training set (void add_training_sample(const ME_Sample & mes)), they are transformed in Sample: a distinction is made here between the external observations (ME_Sample) and the internal representation of those observations (Sample), inaccessible outside the ME_Model.

During this transformation, since it's easier to handle integers in place of strings, then a common trick is to map each string label (and each features) to an integer identifier using an hash map:

Hash implementation

By default, pre-processor instructions in maxent.h call the header ext/hash_map. This implementation of hash table was one the first largely used. However, this is now deprecated. Thus, compiling the project using this kind of hash lead to a warning with a C++11 compiler. As indicated in the source, the best way to skip the warning is to comment the macro which defines USE_HASH_MAP.

#define USE_HASH_MAP  // if you encounter errors with hash, try commenting out this line.  (the program will be a bit slower, though)
#ifdef USE_HASH_MAP
#include <ext/hash_map>
#endif

As the comments indicate, the program will be a bit slower. This is expected since the standard library container map orders its keys. A better alternative would be to use an unordered_map. Therefore, a custom hash function is provided and allows to obtain significant speed improvements (even over the C++11 unordered_map). The structure hashfun_str is used for this definition, into the scope of MiniStringBag.

#ifdef USE_HASH_MAP
    typedef __gnu_cxx::hash_map<std::string, int, hashfun_str> map_type;
#else
    typedef std::map<std::string, int> map_type;
#endif

By default, the ext/hash_map implementation cannot deal with string keys. This is partly because this hash_map is not a part of the standard library. Thus, in order to records labels and features as keys, it is necessary to give a hash function to handle the string. This is the goal of the hashfun_str structure which is an function object. As we can read into (Stroupstrup, 1997):

An object of a class with an application operator (§11.9) is called a function-like object, a functor or simply a function object. (18.4, Stroupstrup, 1997)

  struct hashfun_str
  {
    size_t operator()(const std::string& s) const {
      assert(sizeof(int) == 4 && sizeof(char) == 1);
      const int* p = reinterpret_cast<const int*>(s.c_str());
      size_t v = 0;
      int n = s.size() / 4;
      for (int i = 0; i < n; i++, p++) {
        v ^= *p << (4 * (i % 2)); // note) 0 <= char < 128
      }
      int m = s.size() % 4;
      for (int i = 0; i < m; i++) {
        v ^= s[4 * n + i] << (i * 8);
      }
      return v;
    }
  };

As we can see, this hash function uses extensively low-level bitwise operations, in order to obtain significant speed improvements (see benchmark directory). This can done since it's possible to have some insights about the data.

Constituting the training set

The function add_training_sample(const ME_Sample & mes) transforms a ME_Sample into a Sample. The samples are, internally to each model, stored into a vector of training samples (std::vector<Sample> _vs). The string representing the feature of the ME_Sample are transformed into their corresponding integer.

Different objects are proposed:

  std::vector<Sample> _vs; // vector of training_samples
  StringBag _label_bag;
  MiniStringBag _featurename_bag;
  std::vector<double> _vl;  // vector of lambda
  ME_FeatureBag _fb;
  int _num_classes;
  std::vector<double> _vee;  // empirical expectation
  std::vector<double> _vme;  // empirical expectation
  std::vector< std::vector< int > > _feature2mef;

An active feature is a pair of feature-label identifiers contained in the structure ME_Feature. Internally, each one is casted into a single unsigned int. The label identifier is stored on the first 8 bits, and the 24 remaining are dedicated to represent the feature identifier. For instance, the ME_Feature of the label 3 and the feature 7 is represented as:

00000000000000000000011100000011

Then, in this implementation, we can have, at most, 256 labels and 2^24 features.

FeatureBag

Two data structures are involved in ME_FeatureBag:

• Hash implementation with pairs <unsigned int, int> called mef2id

• Standard vector of ME_Features, called id2mef.

Note that mef probably stands for ME_Feature.

Two functions are defined for FeatureBag:

• The put function:

int Put(const ME_Feature & i) {
  map_type::const_iterator j = mef2id.find(i.body());
  if (j == mef2id.end()) {
    int id = id2mef.size();
    id2mef.push_back(i);
    mef2id[i.body()] = id;
    return id;
  }
  return j->second;
}

Example

We can imagine a simple example.

    ME_Sample s1("CLASS_A");
    s1.add_feature("x1");
    s1.add_feature("x2");
    s1.add_feature("x3", 4.0);

    ME_Sample s2("CLASS_A");
    s2.add_feature("x2");
    s2.add_feature("x3", 5.0);
    s2.add_feature("x4", 1.0);

    ME_Sample s3("CLASS_B");
    s3.add_feature("x1");
    s3.add_feature("x3", 1.0);
    s3.add_feature("x4", 3.0);

At the beginning, our training set has the following form:

samples	x1	x2	x3	x4	y
s1	1	1	4.0		CLASS_A
s2		1	5.0	1.0	CLASS_A
s3	1		1.0	3.0	CLASS_B

And we have 7 active features:

classes	x1	x2	x3	x4
CLASS_A	x	x	x	x
CLASS_B	x		x	x

After the computing of empirical expectation, also known as observations counts we obtain the following distribution:

classes	x1	x2	x3	x4
0	1	2	9	1
1	1		1	3

Each value are divided by the size of training set.

classes	x1	x2	x3	x4
0	0.333	0.666	3	0.333
1	0.333		0.333	1

Optimization methods

By default, this library uses LBFGS to optimize the objective.