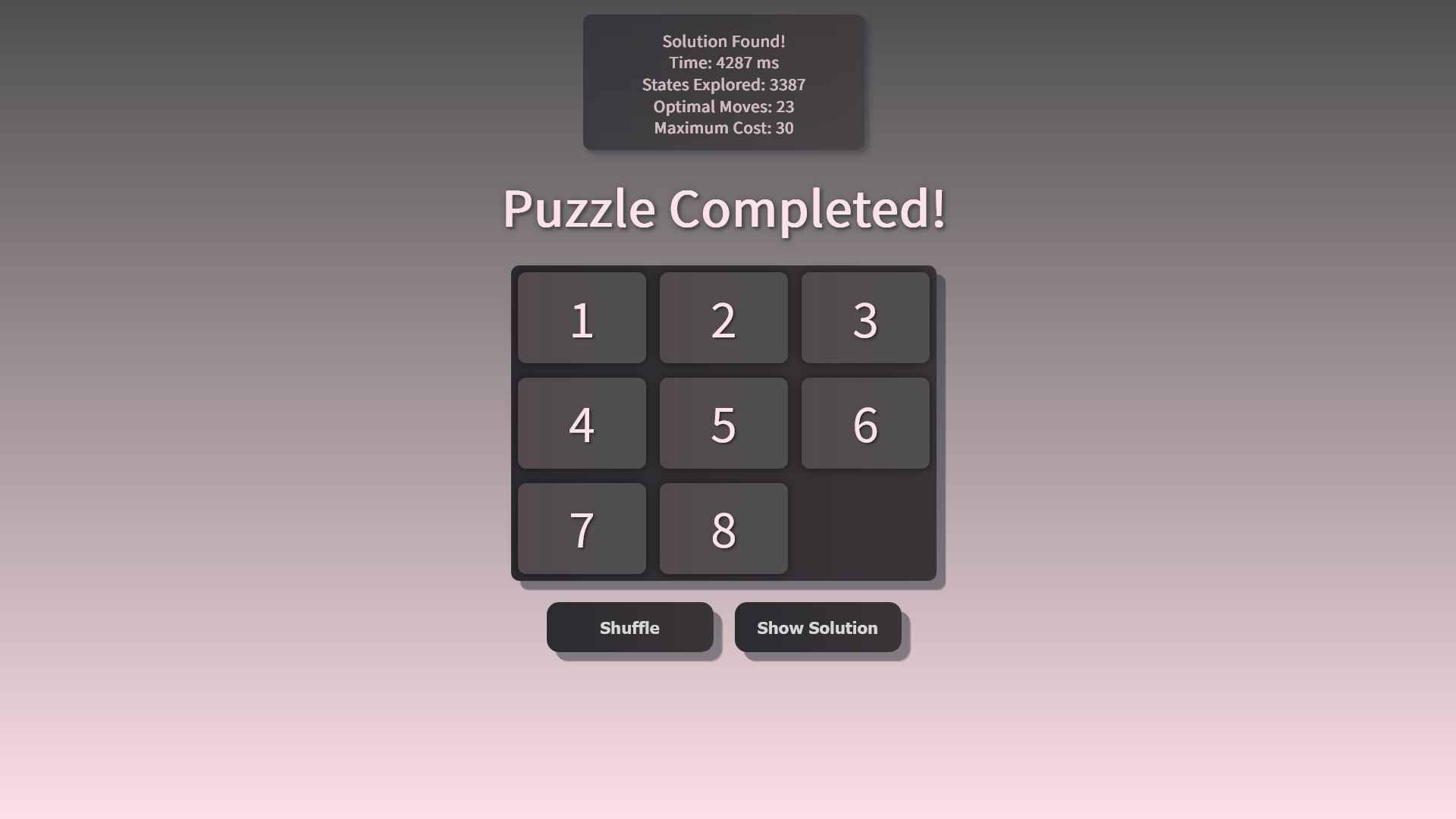
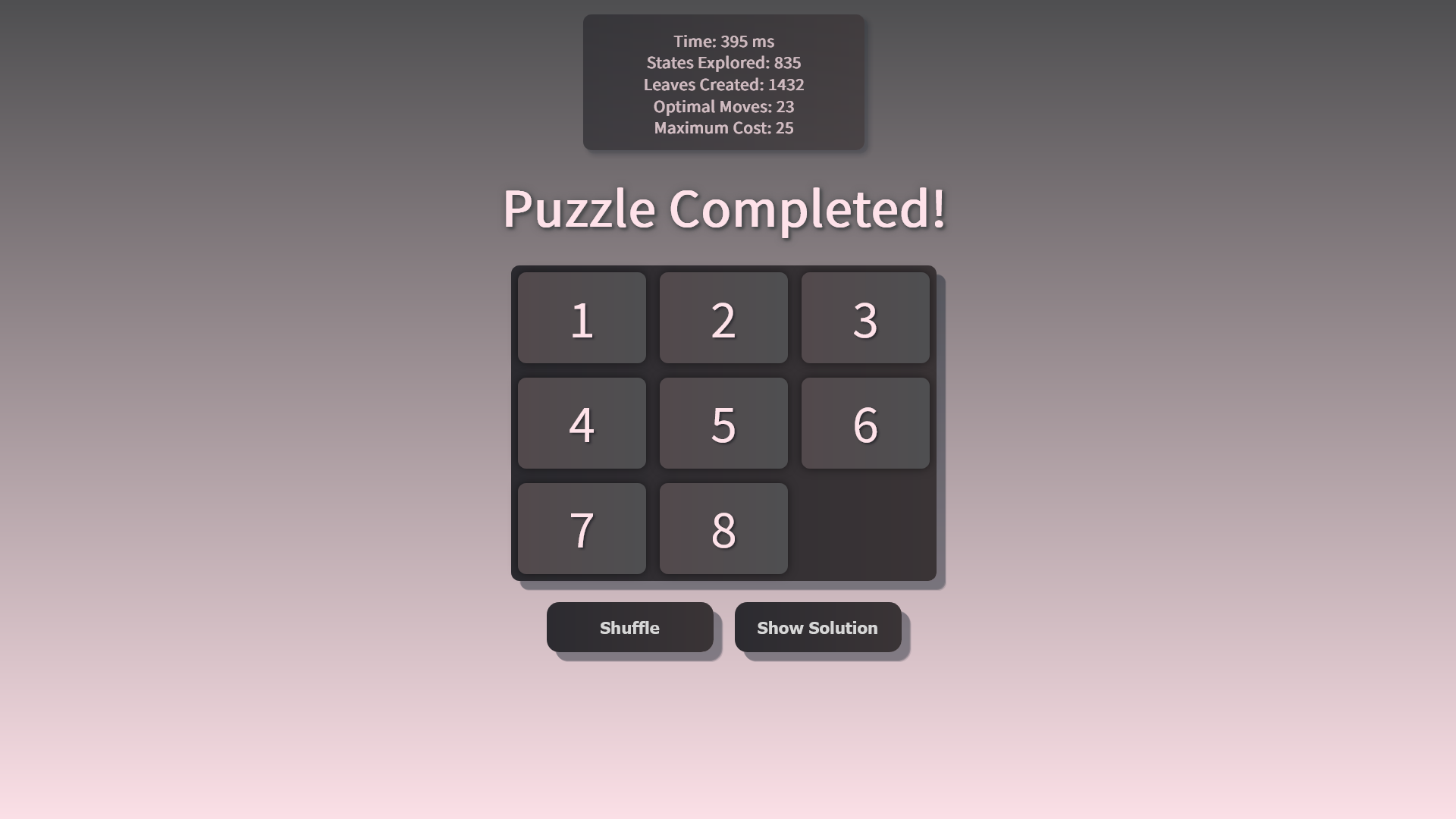
Using A* Algorithm to find the shortest solution to the 8 Puzzle.
-- Given a 3x3 board with 8 tiles (1 to 8) and one empty space. The objective is to place the numbers on tiles to match final configuration using the empty space. We can slide four adjacent (left, right, above and below) tiles into the empty space.
The problem can be mapped into a search problem as follows:
- State space: All possible configurations of the given board
- Initial state: The given board with one tile missing
- Goal state: The final configuration of the board
- Successor function: All possible moves that can be made from a given state
- Path cost: Number of moves so far to reach the current state
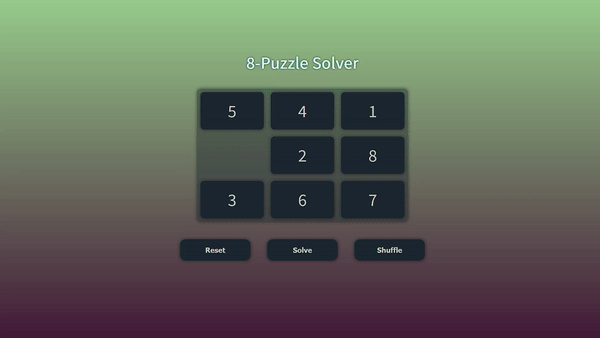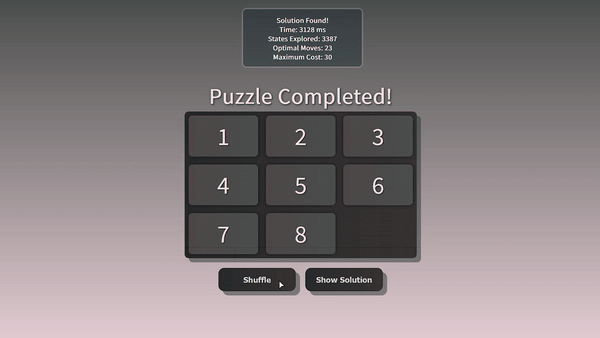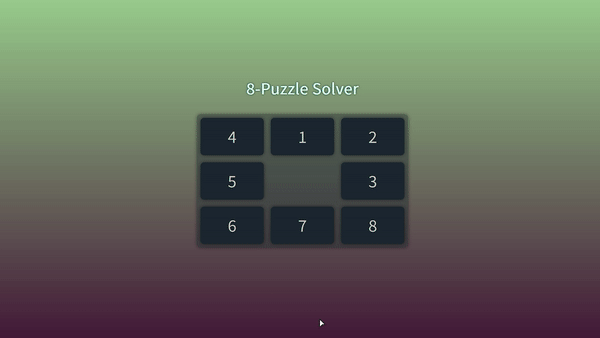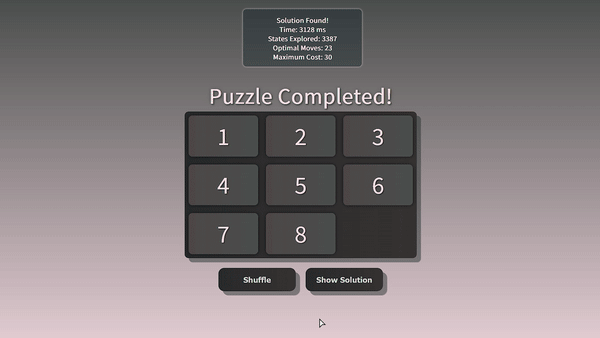
For this problem, we will use A* algorithm to find the shortest path from the initial state to the goal state. There's better algorithm like IDA* but it's not implemented in this project. The algorithm is as follows:
- Create a decision tree with the initial state as the root node
- Expand the node with the lowest f(n) value
- Repeat until the goal state is reached or the tree is exhausted
The heuristic function is used to calculate the cost of a given state. The cost is calculated by finding the distance of each tile from its goal position. The distance is calculated based on their row and column position, only taking into account the number of moves required to reach the goal position.
- Clone the repository
- Open index.html in your browser and the app will run.
Notes:
- The app is not optimized for mobile devices yet. But it will work on mobile devices.
- If a solution is not found, the app will show a message saying "No solution found". However, the app will still run in the background, if it's taking too long to find a solution, I suggest you refresh the page.
- If needed a custom board can be created by changing the initial state in the code, or using the drawGrid() function in the console, which takes an Int Array as input.