README.md

Markov Solver

Utility to solve Markov Chains.

Requirements

• Python 3.6+
• graphviz 12.0.0

Install

pip install markov-solver

Usage

You can use markov-solver as a CLI or as a library in your project.

To use it as a CLI, check the recorded demo:

To use it as a library, you can check the examples.

In both cases you need to define the Markov Chain to solve. See the instructions below to know how to do it.

Chain with constant transition rates

Let us image that we want to solve the following Markov chain:

We should create a YAML file that defines the chain:

chain:
  - from: "Sunny"
    to: "Sunny"
    value: "0.9"

  - from: "Sunny"
    to: "Rainy"
    value: "0.1"

  - from: "Rainy"
    to: "Rainy"
    value: "0.5"

  - from: "Rainy"
    to: "Sunny"
    value: "0.5"

Then, running the following command:

markov-solver solve --definition [PATH_TO_DEFINITION_FILE]

We obtain the following result:

===============================================================
                     MARKOV CHAIN SOLUTION
===============================================================

                      states probability
Rainy.........................................0.166666666666667
Sunny.........................................0.833333333333333

Chain with symbolic transition rates

Let us image that we want to solve the following Markov chain:

We should create a YAML file that defines the chain:

symbols:
  lambda: 1.5
  mu: 2.0

chain:
  - from: "0"
    to: "1"
    value: "lambda"

  - from: "1"
    to: "2"
    value: "lambda"

  - from: "2"
    to: "3"
    value: "lambda"

  - from: "3"
    to: "2"
    value: "3*mu"

  - from: "2"
    to: "1"
    value: "2*mu"

  - from: "1"
    to: "0"
    value: "mu"

Then, running the following command:

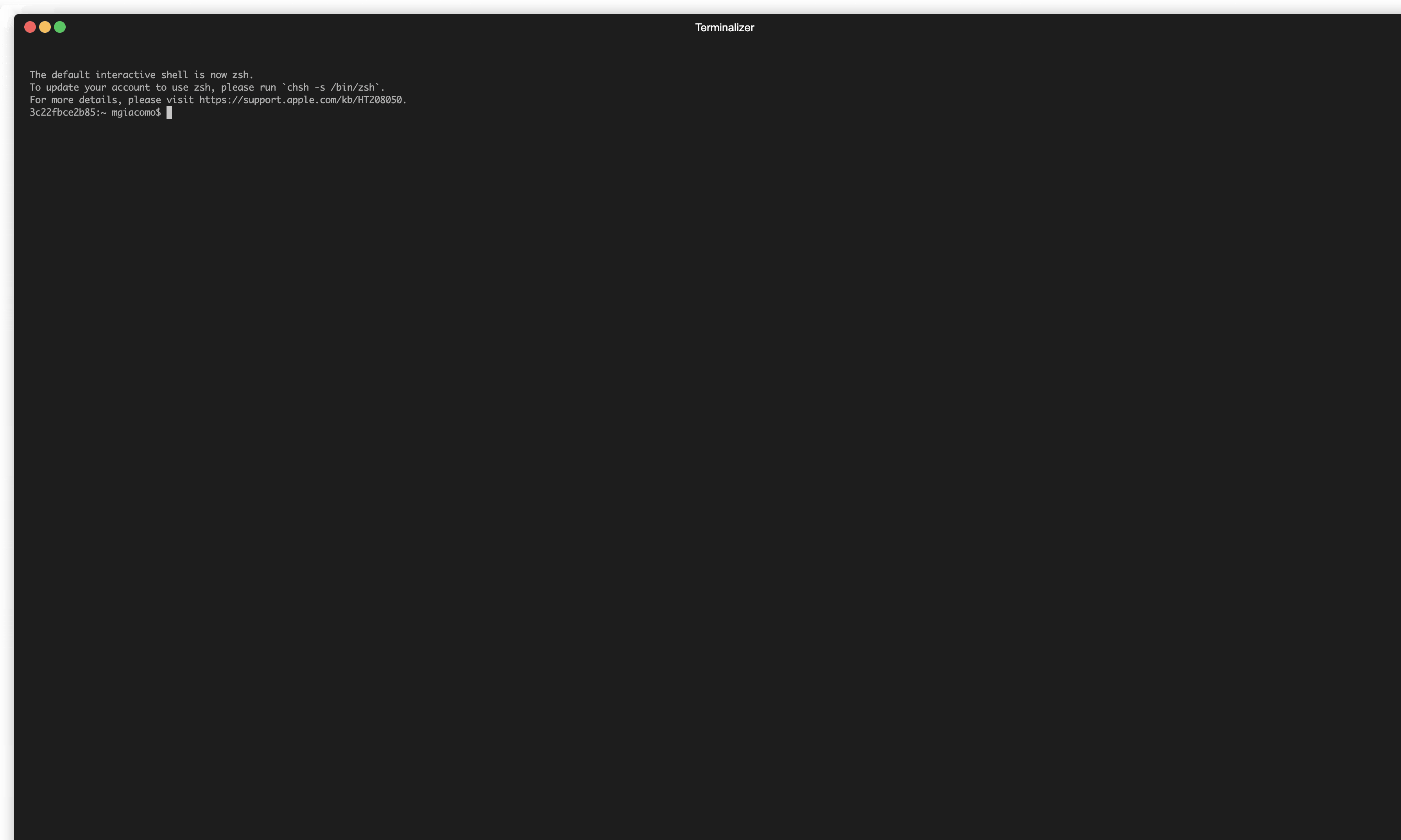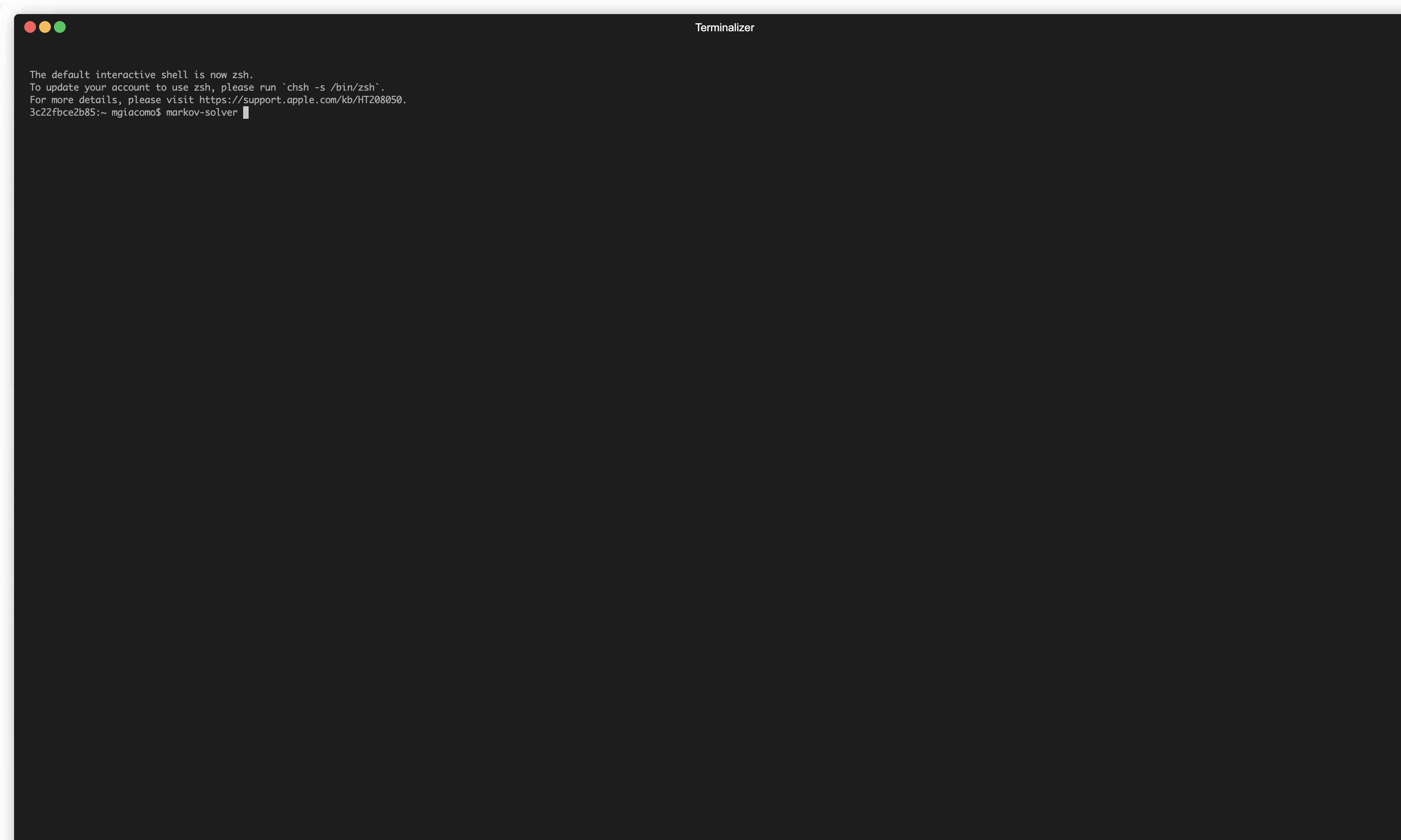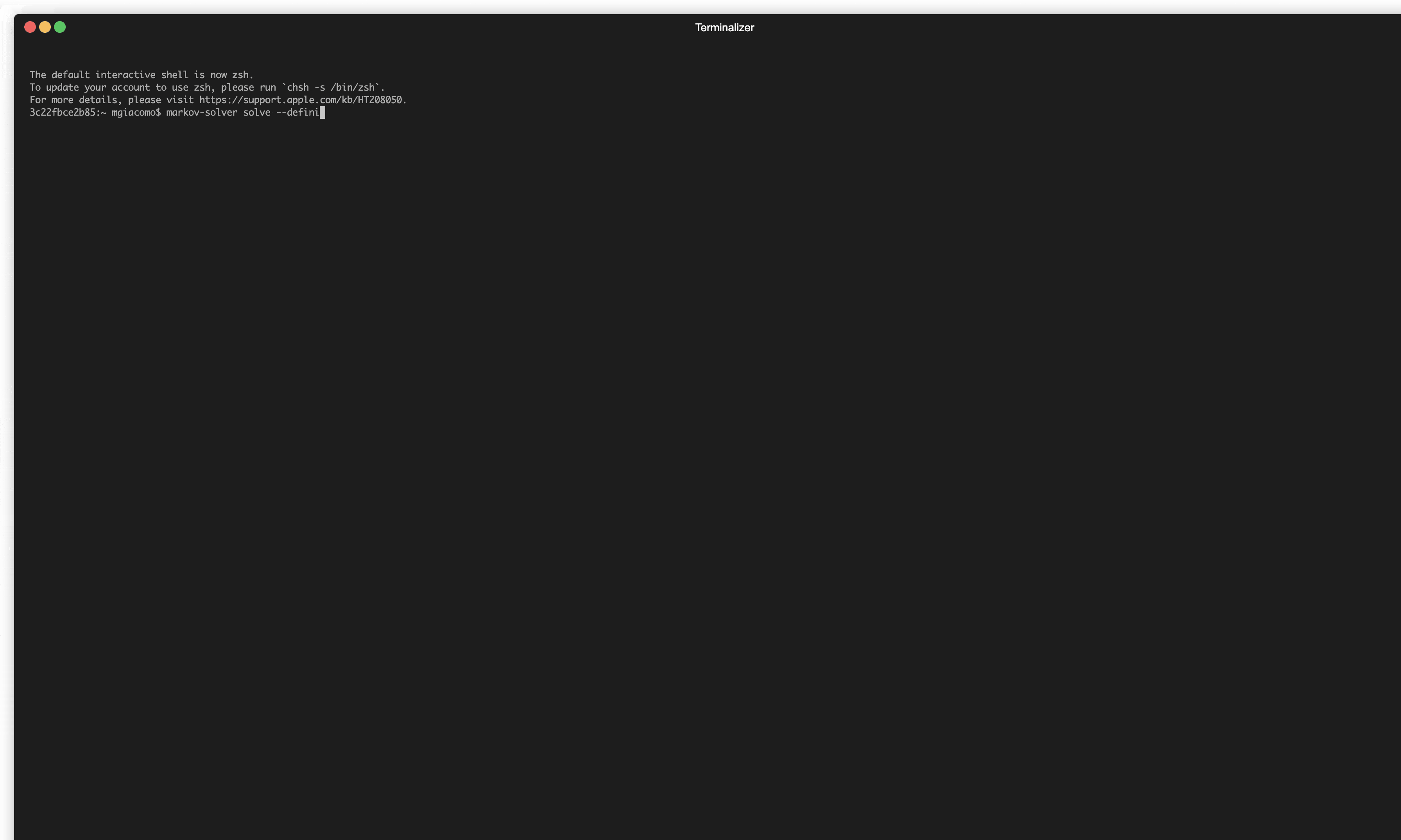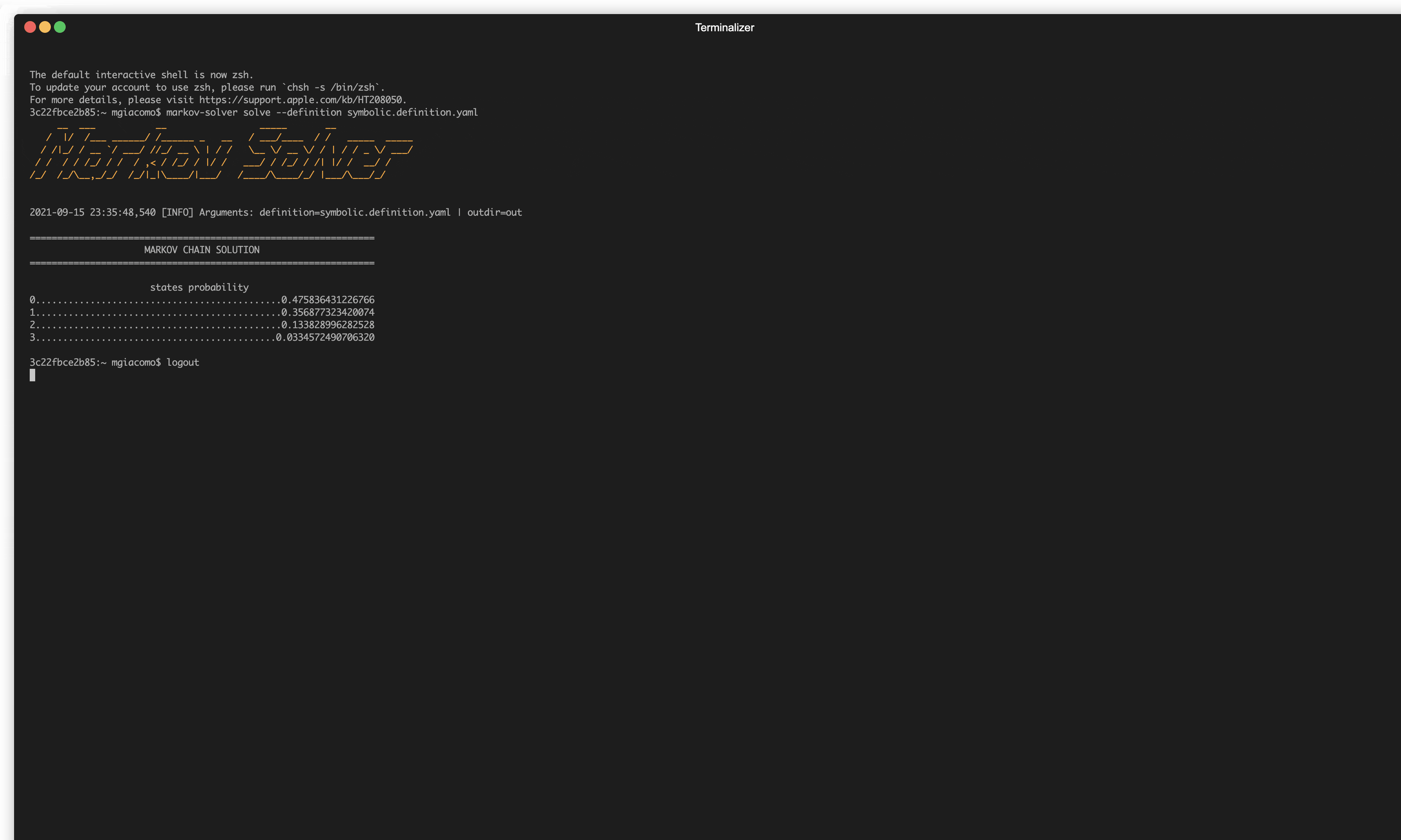
markov-solver solve --definition [PATH_TO_DEFINITION_FILE]

We obtain the following result:

===============================================================
                     MARKOV CHAIN SOLUTION
===============================================================

                      states probability
0.............................................0.475836431226766
1.............................................0.356877323420074
2.............................................0.133828996282528
3............................................0.0334572490706320

Authors

Giacomo Marciani, [email protected]

References

• "Discrete-Event Simulation", 2006, L.M. Leemis, S.K. Park
• "Performance Modeling and Design of Computer Systems, 2013, M. Harchol-Balter

License

The project is released under the MIT License.