README.md

1706. Where Will the Ball Fall

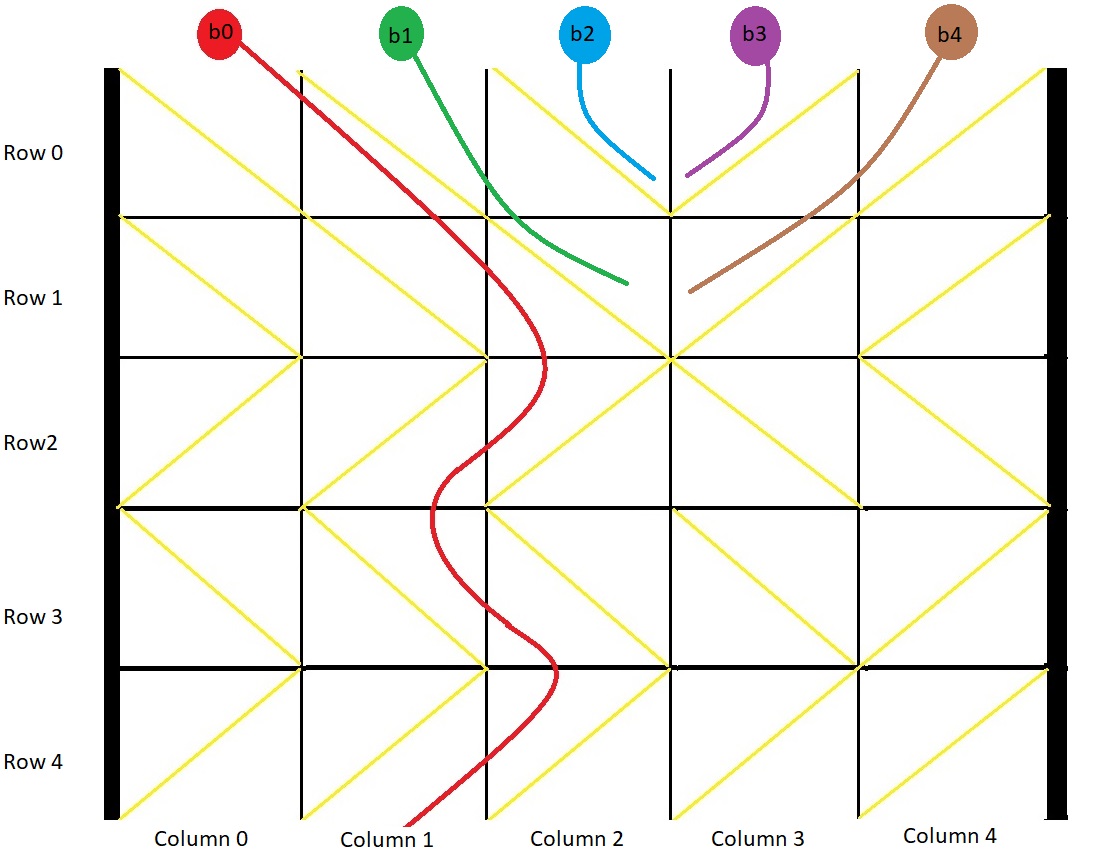
You have a 2-D grid of size m x n representing a box, and you have n balls. The box is open on the top and bottom sides.

Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.

• A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as 1.
• A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as -1.

We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V" shaped pattern between two boards or if a board redirects the ball into either wall of the box.

Return an array answer of size n where answer[i] is the column that the ball falls out of at the bottom after dropping the ball from the ith column at the top, or -1 if the ball gets stuck in the box.

Example 1:

Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
Output: [1,-1,-1,-1,-1]
Explanation: This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.

Example 2:

Input: grid = [[-1]]
Output: [-1]
Explanation: The ball gets stuck against the left wall.

Example 3:

Input: grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
Output: [0,1,2,3,4,-1]

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• grid[i][j] is 1 or -1.

Solutions (Rust)

1. Solution

impl Solution {
    pub fn find_ball(grid: Vec<Vec<i32>>) -> Vec<i32> {
        let n = grid[0].len();
        let mut answer = (0..n as i32).collect::<Vec<_>>();

        for row in &grid {
            for ball in 0..n {
                if answer[ball] != -1 {
                    if row[answer[ball] as usize] == 1
                        && answer[ball] + 1 < n as i32
                        && row[answer[ball] as usize + 1] == 1
                    {
                        answer[ball] += 1;
                    } else if row[answer[ball] as usize] == -1
                        && answer[ball] > 0
                        && row[answer[ball] as usize - 1] == -1
                    {
                        answer[ball] -= 1;
                    } else {
                        answer[ball] = -1;
                    }
                }
            }
        }

        answer
    }
}