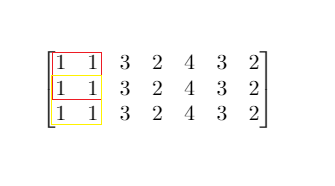
Given a m x n matrix mat and an integer threshold, return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4 Output: 2 Explanation: The maximum side length of square with sum less than 4 is 2 as shown.
Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1 Output: 0
m == mat.lengthn == mat[i].length1 <= m, n <= 3000 <= mat[i][j] <= 1040 <= threshold <= 105
import bisect
class Solution:
def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
m, n = len(mat), len(mat[0])
prefixsum = [[0] * n for _ in range(m)]
ret = 0
for i in range(m):
for j in range(n):
prefixsum[i][j] = mat[i][j]
prefixsum[i][j] += prefixsum[i - 1][j] if i > 0 else 0
prefixsum[i][j] += prefixsum[i][j - 1] if j > 0 else 0
prefixsum[i][j] -= prefixsum[i - 1][j - 1] \
if i > 0 and j > 0 else 0
lengths = list(range(1, min(i, j) + 2))
length = bisect.bisect_right(
lengths, threshold, key=lambda k: self.f(prefixsum, i, j, k))
ret = max(ret, length)
return ret
def f(self, prefixsum, i, j, k):
s = prefixsum[i][j]
s -= prefixsum[i - k][j] if i >= k else 0
s -= prefixsum[i][j - k] if j >= k else 0
s += prefixsum[i - k][j - k] if i >= k and j >= k else 0
return s