README.md

1001. Grid Illumination

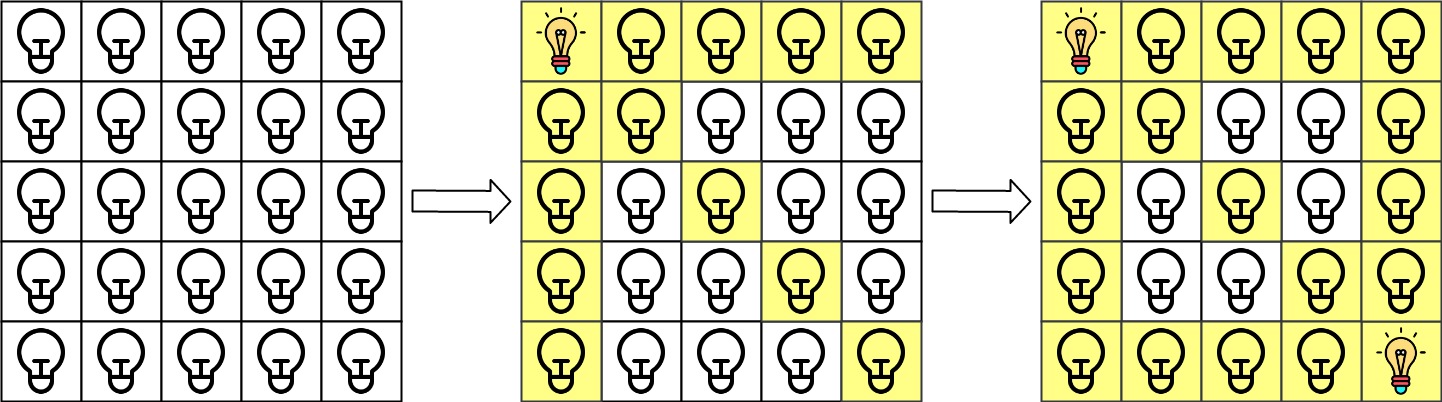
There is a 2D grid of size n x n where each cell of this grid has a lamp that is initially turned off.

You are given a 2D array of lamp positions lamps, where lamps[i] = [rowi, coli] indicates that the lamp at grid[rowi][coli] is turned on. Even if the same lamp is listed more than once, it is turned on.

When a lamp is turned on, it illuminates its cell and all other cells in the same row, column, or diagonal.

You are also given another 2D array queries, where queries[j] = [rowj, colj]. For the jth query, determine whether grid[rowj][colj] is illuminated or not. After answering the jth query, turn off the lamp at grid[rowj][colj] and its 8 adjacent lamps if they exist. A lamp is adjacent if its cell shares either a side or corner with grid[rowj][colj].

Return an array of integers ans, where ans[j] should be 1 if the cell in the jth query was illuminated, or 0 if the lamp was not.

Example 1:

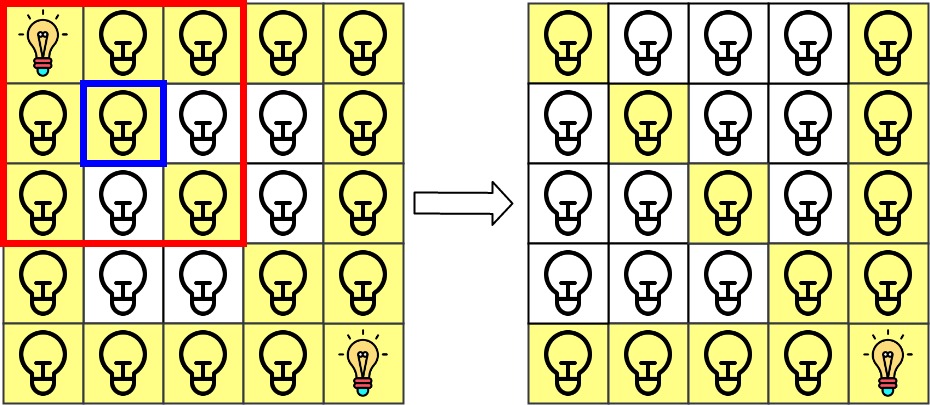
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
Output: [1,0]
Explanation: We have the initial grid with all lamps turned off. In the above picture we see the grid after turning on the lamp at grid[0][0] then turning on the lamp at grid[4][4].
The 0th query asks if the lamp at grid[1][1] is illuminated or not (the blue square). It is illuminated, so set ans[0] = 1. Then, we turn off all lamps in the red square.

The 1st query asks if the lamp at grid[1][0] is illuminated or not (the blue square). It is not illuminated, so set ans[1] = 0. Then, we turn off all lamps in the red rectangle.

Example 2:

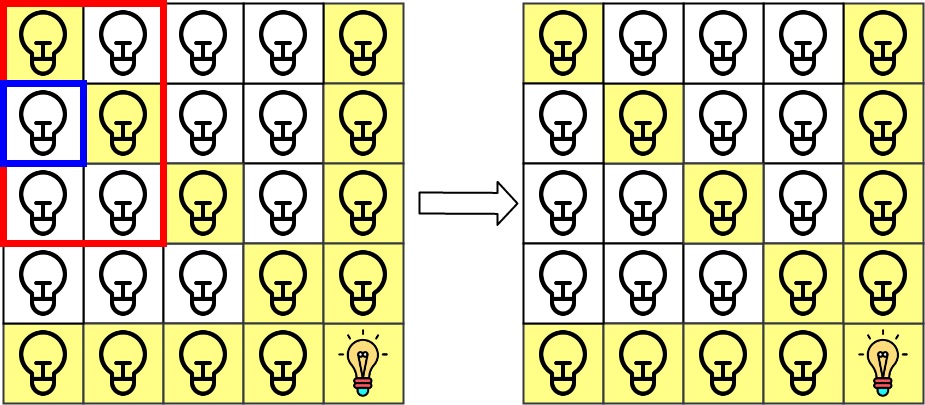
Input: n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
Output: [1,1]

Example 3:

Input: n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
Output: [1,1,0]

Constraints:

• 1 <= n <= 109
• 0 <= lamps.length <= 20000
• 0 <= queries.length <= 20000
• lamps[i].length == 2
• 0 <= rowi, coli < n
• queries[j].length == 2
• 0 <= rowj, colj < n

Solutions (Rust)

1. Solution

use std::collections::HashMap;

impl Solution {
    pub fn grid_illumination(n: i32, lamps: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {
        let mut on_lamps = HashMap::new();
        let mut illuminated_rows = HashMap::new();
        let mut illuminated_cols = HashMap::new();
        let mut illuminated_dias0 = HashMap::new();
        let mut illuminated_dias1 = HashMap::new();
        let mut ans = vec![0; queries.len()];

        for lamp in &lamps {
            let row = lamp[0];
            let col = lamp[1];
            let dia0 = row - col;
            let dia1 = row + col;

            if on_lamps.insert((row, col), (dia0, dia1)).is_none() {
                illuminated_rows
                    .entry(row)
                    .and_modify(|c| *c += 1)
                    .or_insert(1);
                illuminated_cols
                    .entry(col)
                    .and_modify(|c| *c += 1)
                    .or_insert(1);
                illuminated_dias0
                    .entry(dia0)
                    .and_modify(|c| *c += 1)
                    .or_insert(1);
                illuminated_dias1
                    .entry(dia1)
                    .and_modify(|c| *c += 1)
                    .or_insert(1);
            }
        }

        for i in 0..queries.len() {
            let row = queries[i][0];
            let col = queries[i][1];
            let dia0 = row - col;
            let dia1 = row + col;

            ans[i] = (*illuminated_rows.get(&row).unwrap_or(&0) > 0
                || *illuminated_cols.get(&col).unwrap_or(&0) > 0
                || *illuminated_dias0.get(&dia0).unwrap_or(&0) > 0
                || *illuminated_dias1.get(&dia1).unwrap_or(&0) > 0) as i32;

            for x in -1..2 {
                for y in -1..2 {
                    if let Some((dia0, dia1)) = on_lamps.remove(&(row + x, col + y)) {
                        *illuminated_rows.get_mut(&(row + x)).unwrap() -= 1;
                        *illuminated_cols.get_mut(&(col + y)).unwrap() -= 1;
                        *illuminated_dias0.get_mut(&dia0).unwrap() -= 1;
                        *illuminated_dias1.get_mut(&dia1).unwrap() -= 1;
                    }
                }
            }
        }

        ans
    }
}