README.md

790. Domino and Tromino Tiling

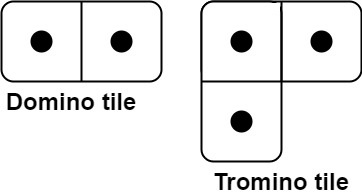
You have two types of tiles: a 2 x 1 domino shape and a tromino shape. You may rotate these shapes.

Given an integer n, return the number of ways to tile an 2 x n board. Since the answer may be very large, return it modulo 109 + 7.

In a tiling, every square must be covered by a tile. Two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Example 1:

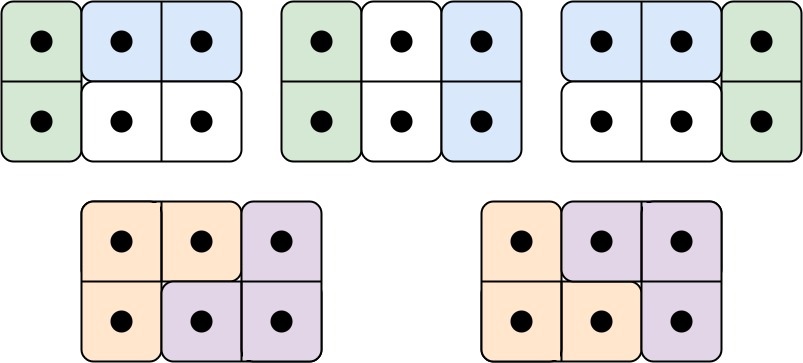
Input: n = 3
Output: 5
Explanation: The five different ways are show above.

Example 2:

Input: n = 1
Output: 1

Constraints:

• 1 <= n <= 1000

Solutions (Rust)

1. Solution

impl Solution {
    pub fn num_tilings(n: i32) -> i32 {
        if n == 1 {
            return 1;
        }

        let mut dp = vec![(0, 0, 0); n as usize];
        dp[0].0 = 1;
        dp[1] = (1, 1, 1);

        for i in 0..n as usize - 1 {
            dp[i + 1].0 = (dp[i].0 + dp[i + 1].0) % 1_000_000_007;
            dp[i + 1].0 = (dp[i].1 + dp[i + 1].0) % 1_000_000_007;
            dp[i + 1].0 = (dp[i].2 + dp[i + 1].0) % 1_000_000_007;
            dp[i + 1].1 = (dp[i].2 + dp[i + 1].1) % 1_000_000_007;
            dp[i + 1].2 = (dp[i].1 + dp[i + 1].2) % 1_000_000_007;
            if i + 2 < n as usize {
                dp[i + 2].0 = (dp[i].0 + dp[i + 2].0) % 1_000_000_007;
                dp[i + 2].1 = (dp[i].0 + dp[i + 2].1) % 1_000_000_007;
                dp[i + 2].2 = (dp[i].0 + dp[i + 2].2) % 1_000_000_007;
            }
        }

        dp[n as usize - 1].0
    }
}