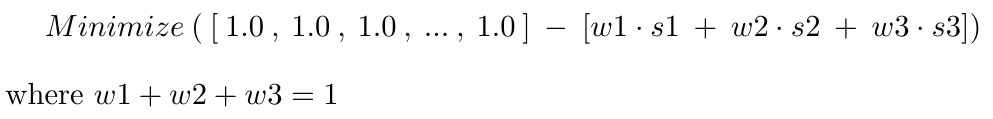This work aims at finding similar tools for the Galaxy tools using a combination of approaches from the field of data mining and machine learning. The script analyses the attributes (like name, description, file types and so on) of tools and extracts keywords (annotations or tokens) which represent the tools. This information is divided into two/three sources - input and output file types and name, description and help text. The keywords are cleaned for stop words in English, special characters and numbers. This pre-processing is necessary in order to construct a set of keywords to better represent a tool. Since these sources do not carry equal weights (they are not equally important in classifying tools) in representing tools, we need to learn weights on these sources of annotations and compute a weighted similarity score for each tool against all tools. This weighting is achieved using an optimizer (Gradient Descent).
- Extract tools' data from GitHub (Galaxy tools).
- Clean the text (For numbers, stop words and special characters).
- Compute the relevant scores for each token (tf-idf, BM25).
- Find similarity in text (Using cosine, jaccard or doc2vec similarity techniques).
- Optimize the combination the similarity scores obtained through multiple sources (Gradient Descent).
Next, for each tool, the relevance score for each token is computed using term frequency and inverted document frequency approach. It is a standard approach to ascertain which keywords are better than the others. It follows Zipf's law - more frequent words are not good representatives of their source. The relevance score of each keyword is computed using the BM25 formula for each tool. Each tool now becomes a vector of keywords (with their relevance scores). Collecting all these vectors for all tools gives us two tools-keywords matrices, one for each source.
The tools-keywords matrices are sparse. It contains relevant scores for each keyword for that tool. But, it misses out on the relevance of occurring a group of words or a concept many times across the tools. If a concept/two or more words occur together multiple times, then it is important to capture that concept. This is achieved by matrix factorization techniques. Singular value decomposition is performed on the tools-keywords matrix (only for the second source comprising of the name, desc. and help text). Now, after decomposition we have three matrices - the middle one is a diagonal matrix (of eigen values). This matrix is sorted in descending order and about 70% (of the total sum of eigen values) is retained and the rest information is discarded (which do not represent important concepts). This reduction percentage is heuristic and based on experiments. After the reduction, the matrices are combined again which approximates the original tools-keywords matrix. The recreated matrix has a lower rank (about 40% of the original rank - keeping just 40% of the original rank helps us keep 70% of the concepts).
After having these tools-keywords matrices, we compute distances between a pair of tools (now vectors) using Jaccard and Cosine distances. Calculating these distances between each pair of tools gives us a two N x N matrices (correlation or similarity matrices). Each row of a similarity matrix (for a source) denotes similarity scores of each tool with the current tool. Every entry in this matrices is a real number between 0 and 1. 0 means complete dissimilarity and 1 means complete similarity. These similarity matrices are normalized to have two similarity distributions. It means that each row in a matrix would sum up to 1.
Now, we have two similarity distributions - there is a question of their optimal combination (a mixture of similarities). A naive way would be to take an average of the similarities. Another (and better) approach is to use an optimizer to learn the optimal weights on these two matrices. It is achieved using Gradient Descent optimizer. The learning rate is computed using Backtracking Line Search. For each tool, two scalar weights are learned for its corresponding vectors in two matrices.
Rather than using cosine angle similarity for documents, a learning-based approach known as doc2vec is used to compute fixed length vector representations (document embeddings) for each document. These vector representations (one for each document) can be used to find its proximity to all other documents using popular vector distance metrics. The basic principle of this work is to predict a word given a set of words. There is a review work of the original work which gives useful insights into the results achieved by the original work. A widely used implementation of this approach is here. We use this approach to find similarity scores among documents and these similarity scores (from multiple sources) are combined using an optimizer for each document.
The results following this approach is here. Another approach which uses latent semantic indexing to find document embedding is here. Please open these links and wait for a few seconds as they load (a big JSON file) a list of tools. Select your favourite tool and browse through the similar tools which are listed in the descending order of their respective similarity scores ('Weighted similarity score' column in the table). Moreover, there are a couple of plots showing the idea of computing optimal combination works better than the average approach. Moreover, they display plots for loss and gradient drop while optimizing the weights.
@inproceedings{rehurek_lrec, title = {{Software Framework for Topic Modelling with Large Corpora}}, author = {Radim {\v R}eh{\r u}{\v r}ek and Petr Sojka}, booktitle = {{Proceedings of the LREC 2010 Workshop on New Challenges for NLP Frameworks}}, pages = {45--50}, year = 2010, month = May, day = 22, publisher = {ELRA}, address = {Valletta, Malta}, note={\url{http://is.muni.cz/publication/884893/en}}, language={English} }