You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
There is already support for BilinearOperator in pyproximal/pyproximal/utils/bilinear.py and the PALM optimizer; however,
they do not scale to second-order methods such as Levenberg-Marquardt (LM) and Variable Projection (VarPro). In recent years, such methods have been become popular alternatives to splitting methods such as ADMM for certain types of problems (e.g. image analysis and computer vision).
Examples
As an example the nuclear norm penalty has a variational formulation
which was utilized in [1] using a bilinear framework (no second order method involved, though).
This also scales to the weighted nuclear norm, and it has been successfully implemented for vision tasks using second-order methods in e.g. [2, 7, 8]. Other non-convex penalties have been studied as well, e.g. [3, 4, 5, 6].
Suggestion on enhancement
I suggest adding support for Levenberg-Marquardt (LM) and Variable Projection (VarPro). As a second step I suggest adding some of the mentioned regularizers.
References
[1] Cabral et al. "Unifying Nuclear Norm and Bilinear Factorization Approaches for Low-Rank Matrix Decomposition", In the Proceedings of the IEEE International Conference on Computer Vision (ICCV), 2013
[2] Iglesias et al. "Accurate Optimization of Weighted Nuclear Norm for Non-Rigid Structure from Motion", In the Proceedings of the European Conference on Computer Vision (ECCV), 2020
[3] Valtonen Ornhag et al. "Bilinear parameterization for differentiable rank-regularization", In the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPR), 2020
[4] Valtonen Ornhag et al. "Differentiable Fixed-Rank Regularisation using Bilinear Parameterisation", In the Proceedings of the British Machine Vision Conference (BMVC), 2019
[5] Valtonen Ornhag et al. "Bilinear Parameterization for Non-Separable Singular Value Penalties", In the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021
[6] Xu et al. "A unified convex surrogate for the schatten-p norm". In Proceedings of the Conference on Artificial Intelligence (AAAI), 2017
[7] Kumar "Non-rigid structure from motion: Prior-free factorization method revisited" In IEEE Winter Conference on Applications of Computer Vision (WACV), 2020
[8] McDonald et al. "Spectral k-support norm regularization", In Advances in Neural Information Processing Systems (NIPS), 2014
The text was updated successfully, but these errors were encountered:
Wow, this looks very interesting! I think you definitely know more in this area, I am quite new to low-rank optimization and all its possibilities. Would you like to have a go at this?
Yes, I would like to look into this; however, there might be some architectural designs to discuss prior to doing the actual implementations. Let me look into it, and I will return with my findings.
There is already support for BilinearOperator in
pyproximal/pyproximal/utils/bilinear.pyand the PALM optimizer; however,they do not scale to second-order methods such as Levenberg-Marquardt (LM) and Variable Projection (VarPro). In recent years, such methods have been become popular alternatives to splitting methods such as ADMM for certain types of problems (e.g. image analysis and computer vision).
Examples
As an example the nuclear norm penalty has a variational formulation
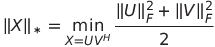
which was utilized in [1] using a bilinear framework (no second order method involved, though).
This also scales to the weighted nuclear norm, and it has been successfully implemented for vision tasks using second-order methods in e.g. [2, 7, 8]. Other non-convex penalties have been studied as well, e.g. [3, 4, 5, 6].
Suggestion on enhancement
I suggest adding support for Levenberg-Marquardt (LM) and Variable Projection (VarPro). As a second step I suggest adding some of the mentioned regularizers.
References
[1] Cabral et al. "Unifying Nuclear Norm and Bilinear Factorization Approaches for Low-Rank Matrix Decomposition", In the Proceedings of the IEEE International Conference on Computer Vision (ICCV), 2013
[2] Iglesias et al. "Accurate Optimization of Weighted Nuclear Norm for Non-Rigid Structure from Motion", In the Proceedings of the European Conference on Computer Vision (ECCV), 2020
[3] Valtonen Ornhag et al. "Bilinear parameterization for differentiable rank-regularization", In the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPR), 2020
[4] Valtonen Ornhag et al. "Differentiable Fixed-Rank Regularisation using Bilinear Parameterisation", In the Proceedings of the British Machine Vision Conference (BMVC), 2019
[5] Valtonen Ornhag et al. "Bilinear Parameterization for Non-Separable Singular Value Penalties", In the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021
[6] Xu et al. "A unified convex surrogate for the schatten-p norm". In Proceedings of the Conference on Artificial Intelligence (AAAI), 2017
[7] Kumar "Non-rigid structure from motion: Prior-free factorization method revisited" In IEEE Winter Conference on Applications of Computer Vision (WACV), 2020
[8] McDonald et al. "Spectral k-support norm regularization", In Advances in Neural Information Processing Systems (NIPS), 2014
The text was updated successfully, but these errors were encountered: